[기계학습/인공지능] Probabilistic Model
#기계학습#딥러닝#머신러닝#인공지능#정보시스템공학과#컴퓨터공학과 #largemarginmethod #이론공부#학교공부
https://wikidocs.net/24958 / https://knowable.tistory.com/46?category=931709
의 글과 사진을 참고하였습니다. 문제가 있을 시 삭제하겠습니다.
https://blog.naver.com/haein0758/222765310556 동일 작성자입니다.
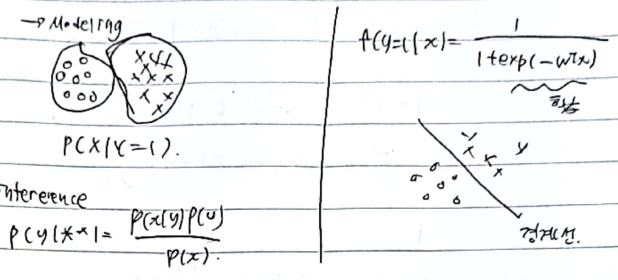
1. Generative method vs discrimative method
각각 일반적으로 분류하는 모델과, 경계선을 찾아 class를 분류하는 모델이다. 이번 포스팅은 주로 generative method 에 대해 작성할 것이다.
2. Probability
ratio of cordinality : p(x=a), p(x=a | y=c) 일때를 각각 구하겠다. 일반적으로 우리가 알고 있는 확률, 조건부 확률이라고 생각하면 된다.

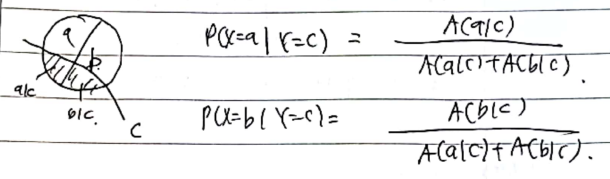
Probability density p VS Probability P
1) x는 continous(연속형) 변수일때, p(x)>=0 for all x(모집단에 포함된)
2) p(x)dx를 적분하면 모든 확률값들을 넓이로 표현하는 것이므로 그 값은 1이다.
기댓값
x가 continous일때 f(x)*p(x) 곱한 값을 적분해주면 된다.
joint pdf : p(x1, x2)
conditional pdf : p(x1 | x2)
marginal pdf : p(x1) = p(x1,x2)를 dx2로 적분
*marginal pdf : x2의 값으로 1과 2밖에 없다고 가정시,
p(x1=1) = p(x1=1, x2=1) + p(x1=1, x2=2) >> p(x1,x2)를 dx2로 적분한값괃 ㅗㅇ일하게 된다.
Bayes's rule


이를 x1, x2, x3를 확률변수로 가지는 분포에 대해 적용을 하고 margin pdf와 비교하겠다.

example)
y(옷가격) 예측을 위해 확률변수 (x1: 색상, x2: 가격, x3: 원단, x4:사이즈) x가 있다.
이때 x1이 주어지지 않을 때 x1의 marginal pdf를 구하는 방법은 다음과 같다.

3. Gaussian pdf
가우시안 분포는 다음과 같다. 정규분포 공식이다

이를 행렬식으로 표현하자면 다음과 같다.
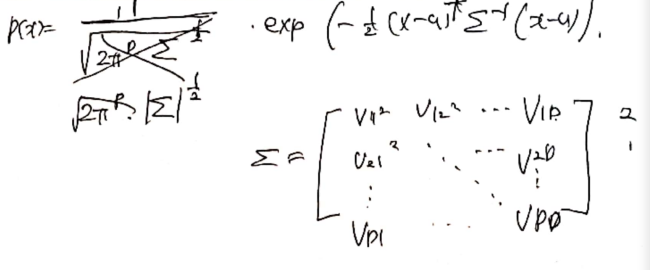
from orginal multivariate gaussian pdf

라고 할 수 있다. u와 공분산은 다음과 같이 정리된다.